Tuesday, 16 August 2016

Solving the weasel keygenme by kao


Over at tuts4you kao posted a nice .net keygenme. The ultimate goal is developing a keygen which can generate keys for any name within a second.

Know thy goal
Fig 1: Know thy goal

Although the post is titled as "Solving the weasel keygenme", I did not get that far as developing a working keygen as required for the much coveted gold medal. However, the algorithm that kao implements is quite interesting to document and that is the reason for this blog post.

Solving the keygenme consists of two parts -- First to devirtualize the virtual machine and second to reverse the crypto.

De-virtualizing the VM


Dropping the file in dnSpy, reveals that method and variable names have been removed as in Fig 2.

Wazzup with those names?
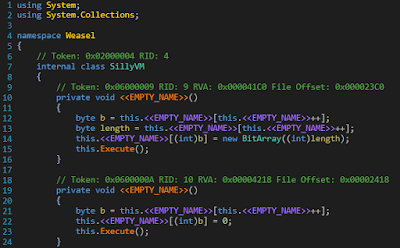Fig 2: Wazzup with those names?
The obfuscation can be removed by processing the file with de4dot which leads to a slightly better readable code as in Fig 3.

Not anonymous anymore
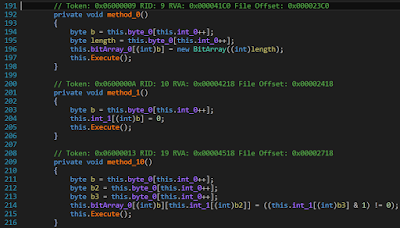Fig 3: Not anonymous anymore
Now with the obfuscation out of the way, it's time to deal with the vm. A vm based software protection works by transforming the original instructions to a set of new instruction which only a custom vm understands. Executing the new set of instructions under the supervision of the vm is expected to produce the same output as executing the original instructions without the vm. As regards to the implementation of a vm this keygenme is also no different.

The virtual machine is implemented in a class named SillyVM. The constructor of this class initializes the opcode handler table as shown in Fig 4. There are 16 instructions that the vm understands.

Initializing the vm
Fig 4: Initializing the vm
Immediately, after setting up the opcode handler table the constructor initializes an array which contains the actual instructions of the vm as shown in Fig 5.
The instructions of the vm
Fig 5: The instructions of the vm
The next task is to understand the semantics of each of the 16 handlers. This is a manual task but it cannot be avoided. Understanding the operation of the handlers is crucial in comprehending the operation of the vm. Luckily, this is not a too difficult task, as the handlers are short and simple. The handlers can then be renamed as per their semantics. As shown in Fig 6, we have renamed three of the handlers to JumpIfLess, JumpIfZero, Multiply.

Renaming the handlers
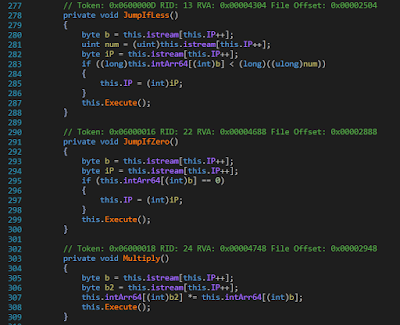Fig 6: Renaming the handlers
The complete set of handlers along with their associated semantics is listed in the following table.

INSTRUCTION OPCODE FORMAT SEMANTICS
Add 0 Add b1, b2 arr[b2] += arr[b1]
JumpIfEqual 1 JumpIfEqual b1, b2, b3 If (arr[b1] == b2) then IP = b3
NewBitArray 2 NewBitArray b1, b2 bitarr[b1] = new BitArray(b2)
JumpIfLess 3 JumpIfLess b1, b2, b3 If (arr[b1] < b2) then IP = b3
JumpIfLargePassw 4 JumpIfLargePassw b1, b2 If (arr[b1] < passw.Length) then IP = b2
Jump 5 Jump b1 IP = b1
JumpIfZero 6 JumpIfZero b1, b2 If (arr[b1] == 0) then IP = b2
BitToInt 7 BitToInt b1, b2, b3 arr[b3] = (bitarr[b1][arr[b2]] == true ? 1 : 0)
Increment 8 Increment b1 arr[b1]++
IndexOf 9 IndexOf b1, b2 arr[b2] = hardc.IndexOf(passw[arr[b1]])
SumNumOne 10 SumNumOne b1, b2 arr[b2] = arr[b1] + 1
Multiply 11 Multiply b1, b2 arr[b2] *= arr[b1]
BitArrayCopy 12 BitArrayCopy b1 bitarr[b1].CopyTo(ans)
IntToBit 13 IntToBit b1, b2, b3 bitarr[b1][arr[b2]] = arr[b3] & 1
RShr 14 RShr b1 arr[b1] >>= 1
SetZero 15 SetZero b1 arr[b1] = 0

As per the above table, we can code a disassembler in python which takes in the instruction list and emits the de-virtualized C# code.
instr = [2,2,56,15,41,15,15,5,36,9,15,8,1,8,255,34,15,1,
5,30,13,2,41,8,8,41,14,8,8,1,3,1,5,20,8,15,4,15,
9,2,1,40,15,61,15,55,15,24,5,134,7,0,61,36,8,61,
15,18,5,78,7,0,61,19,6,19,74,7,2,18,19,0,19,36,8,
61,8,18,3,18,50,60,15,11,5,122,10,11,47,5,116,7,0,
61,19,6,19,112,7,2,11,19,7,2,47,57,11,19,57,0,57,
36,8,61,8,47,3,47,50,91,8,11,3,11,49,86,13,1,55,
36,8,55,8,24,3,24,40,50,12,1]


def disassemble():
 ip = 0
 while ip < len(instr):
  opcode = instr[ip]
  print 'loc_%03d:\t' %(ip),
  ip += 1

  # Add
  if opcode == 0:
   b1 = instr[ip]
   b2 = instr[ip+1]
   ip += 2
   print 'arr[%d] += arr[%d];' %(b2, b1)
   
  # JumpIfEqual
  elif opcode == 1:
   b1 = instr[ip]
   b2 = instr[ip+1]
   b3 = instr[ip+2]
   ip += 3
   print 'if (arr[%d] == (int)((sbyte)%d)) goto loc_%03d;' %(b1, b2, b3)

  # NewBitArray
  elif opcode == 2:
   b1 = instr[ip]
   b2 = instr[ip+1]
   ip += 2
   print 'bitarr[%d] = new BitArray(%d);' %(b1, b2)
  
  # JumpIfLess
  elif opcode == 3:
   b1 = instr[ip]
   b2 = instr[ip+1]
   b3 = instr[ip+2]
   ip += 3
   print 'if ((long)arr[%d] < (long)((ulong)%d)) goto loc_%03d;' %(b1, b2, b3)
  
  # JumpIfLargePassw
  elif opcode == 4:
   b1 = instr[ip]
   b2 = instr[ip+1]
   ip += 2
   print 'if (arr[%d] < password.Length) goto loc_%03d;' %(b1, b2)

  # Jump
  elif opcode == 5:
   b1 = instr[ip]
   ip += 1
   print 'goto loc_%03d;' %(b1)

  # JumpIfZero
  elif opcode == 6:
   b1 = instr[ip]
   b2 = instr[ip+1]
   ip += 2
   print 'if (arr[%d] == 0) goto loc_%03d;' %(b1, b2)

  # BitToInt
  elif opcode == 7:
   b1 = instr[ip]
   b2 = instr[ip+1]
   b3 = instr[ip+2]
   ip += 3
   print 'arr[%d] = (bitarr[%d][arr[%d]] == true ? 1:0);' %(b3, b1, b2)

  # Increment
  elif opcode == 8:
   b1 = instr[ip]
   ip += 1
   print 'arr[%d]++;' %(b1)

  # IndexOf
  elif opcode == 9:
   b1 = instr[ip]
   b2 = instr[ip+1]
   ip += 2
   print 'arr[%d] = "23456789ABCDEFGHJKLMNPQRSTUVWXYZ".IndexOf(password[arr[%d]]);' %(b2, b1)

  # SumNumOne
  elif opcode == 10:
   b1 = instr[ip]
   b2 = instr[ip+1]
   ip += 2
   print 'arr[%d] = arr[%d] + 1;' %(b2, b1)

  # Multiply
  elif opcode == 11:
   b1 = instr[ip]
   b2 = instr[ip+1]
   ip += 2
   print 'arr[%d] *= arr[%d];' %(b2, b1)

  # BitArrayCopy
  elif opcode == 12:
   b1 = instr[ip]
   ip += 1
   print 'bitarr[%d].CopyTo(ans, 0);' %(b1)

  # IntToBit
  elif opcode == 13:
   b1 = instr[ip]
   b2 = instr[ip+1]
   b3 = instr[ip+2]
   ip += 3
   print 'bitarr[%d][arr[%d]] = ((arr[%d] & 1) != 0);' %(b1, b2, b3)

  # RShr
  elif opcode == 14:
   b1 = instr[ip]
   ip += 1
   print 'arr[%d] = (int)((uint)arr[%d] >> 1);' %(b1, b1)

  # SetZero
  elif opcode == 15:
   b1 = instr[ip]
   ip += 1
   print 'arr[%d] = 0;' %(b1)

  else:
   print 'Error'
   break

if __name__ == '__main__':
 disassemble()

Running the disassembler produces the following C# code.
loc_000: bitarr[2] = new BitArray(56);
loc_003: arr[41] = 0;
loc_005: arr[15] = 0;
loc_007: goto loc_036;
loc_009: arr[8] = "23456789ABCDEFGHJKLMNPQRSTUVWXYZ".IndexOf(password[arr[15]]);
loc_012: if (arr[8] == -1) goto loc_034;
loc_016: arr[1] = 0;
loc_018: goto loc_030;
loc_020: bitarr[2][arr[41]] = ((arr[8] & 1) != 0);
loc_024: arr[41]++;
loc_026: arr[8] = (int)((uint)arr[8] >> 1);
loc_028: arr[1]++;
loc_030: if ((long)arr[1] < (long)((ulong)5)) goto loc_020;
loc_034: arr[15]++;
loc_036: if (arr[15] < password.Length) goto loc_009;
loc_039: bitarr[1] = new BitArray(40);
loc_042: arr[61] = 0;
loc_044: arr[55] = 0;
loc_046: arr[24] = 0;
loc_048: goto loc_134;
loc_050: arr[36] = (bitarr[0][arr[61]] == true ? 1:0);
loc_054: arr[61]++;
loc_056: arr[18] = 0;
loc_058: goto loc_078;
loc_060: arr[19] = (bitarr[0][arr[61]] == true ? 1:0);
loc_064: if (arr[19] == 0) goto loc_074;
loc_067: arr[19] = (bitarr[2][arr[18]] == true ? 1:0);
loc_071: arr[36] += arr[19];
loc_074: arr[61]++;
loc_076: arr[18]++;
loc_078: if ((long)arr[18] < (long)((ulong)50)) goto loc_060;
loc_082: arr[11] = 0;
loc_084: goto loc_122;
loc_086: arr[47] = arr[11] + 1;
loc_089: goto loc_116;
loc_091: arr[19] = (bitarr[0][arr[61]] == true ? 1:0);
loc_095: if (arr[19] == 0) goto loc_112;
loc_098: arr[19] = (bitarr[2][arr[11]] == true ? 1:0);
loc_102: arr[57] = (bitarr[2][arr[47]] == true ? 1:0);
loc_106: arr[57] *= arr[19];
loc_109: arr[36] += arr[57];
loc_112: arr[61]++;
loc_114: arr[47]++;
loc_116: if ((long)arr[47] < (long)((ulong)50)) goto loc_091;
loc_120: arr[11]++;
loc_122: if ((long)arr[11] < (long)((ulong)49)) goto loc_086;
loc_126: bitarr[1][arr[55]] = ((arr[36] & 1) != 0);
loc_130: arr[55]++;
loc_132: arr[24]++;
loc_134: if ((long)arr[24] < (long)((ulong)40)) goto loc_050;
loc_138: bitarr[1].CopyTo(ans, 0);

The de-virtualized code thus obtained is semantically equivalent to the original code, but is splattered with numerous gotos. This is because during virtualization the code lost its original structure. Loops were converted to If-then goto statements.  Although we can directly use the code as is, it is better if we try to restore it to its original form which should also improve readability.

Restoring the structure of the de-virtualized code


To restore the original structure of the de-virtualized code we will compile it followed by decompilation with dnSpy.

Original de-virtualized code
void doIt()
{
 bitarr = new BitArray[3];
 bitarr[0] = new BitArray(hardcoded);
 arr = new int[64];
 ans = new byte[5];
 
 loc_000: bitarr[2] = new BitArray(56);
 loc_003: arr[41] = 0;
 loc_005: arr[15] = 0;
 loc_007: goto loc_036;
 loc_009: arr[8] = "23456789ABCDEFGHJKLMNPQRSTUVWXYZ".IndexOf(password[arr[15]]);
 loc_012: if (arr[8] == -1) goto loc_034;
 loc_016: arr[1] = 0;
 loc_018: goto loc_030;
 loc_020: bitarr[2][arr[41]] = ((arr[8] & 1) != 0);
 loc_024: arr[41]++;
 loc_026: arr[8] = (int)((uint)arr[8] >> 1);
 loc_028: arr[1]++;
 loc_030: if ((long)arr[1] < (long)((ulong)5)) goto loc_020;
 loc_034: arr[15]++;
 loc_036: if (arr[15] < password.Length) goto loc_009;
 loc_039: bitarr[1] = new BitArray(40);
 loc_042: arr[61] = 0;
 loc_044: arr[55] = 0;
 loc_046: arr[24] = 0;
 loc_048: goto loc_134;
 loc_050: arr[36] = (bitarr[0][arr[61]] == true ? 1:0);
 loc_054: arr[61]++;
 loc_056: arr[18] = 0;
 loc_058: goto loc_078;
 loc_060: arr[19] = (bitarr[0][arr[61]] == true ? 1:0);
 loc_064: if (arr[19] == 0) goto loc_074;
 loc_067: arr[19] = (bitarr[2][arr[18]] == true ? 1:0);
 loc_071: arr[36] += arr[19];
 loc_074: arr[61]++;
 loc_076: arr[18]++;
 loc_078: if ((long)arr[18] < (long)((ulong)50)) goto loc_060;
 loc_082: arr[11] = 0;
 loc_084: goto loc_122;
 loc_086: arr[47] = arr[11] + 1;
 loc_089: goto loc_116;
 loc_091: arr[19] = (bitarr[0][arr[61]] == true ? 1:0);
 loc_095: if (arr[19] == 0) goto loc_112;
 loc_098: arr[19] = (bitarr[2][arr[11]] == true ? 1:0);
 loc_102: arr[57] = (bitarr[2][arr[47]] == true ? 1:0);
 loc_106: arr[57] *= arr[19];
 loc_109: arr[36] += arr[57];
 loc_112: arr[61]++;
 loc_114: arr[47]++;
 loc_116: if ((long)arr[47] < (long)((ulong)50)) goto loc_091;
 loc_120: arr[11]++;
 loc_122: if ((long)arr[11] < (long)((ulong)49)) goto loc_086;
 loc_126: bitarr[1][arr[55]] = ((arr[36] & 1) != 0);
 loc_130: arr[55]++;
 loc_132: arr[24]++;
 loc_134: if ((long)arr[24] < (long)((ulong)40)) goto loc_050;
 loc_138: bitarr[1].CopyTo(ans, 0);
}

Decompiled code after recompilation 
// Token: 0x06000005 RID: 5 RVA: 0x00003A94 File Offset: 0x00002A94
private void doIt()
{
 this.bitarr = new BitArray[3];
 this.bitarr[0] = new BitArray(this.hardcoded);
 this.arr = new int[64];
 this.ans = new byte[5];
 this.bitarr[2] = new BitArray(56);
 this.arr[41] = 0;
 this.arr[15] = 0;
 while (this.arr[15] < this.password.Length)
 {
  this.arr[8] = "23456789ABCDEFGHJKLMNPQRSTUVWXYZ".IndexOf(this.password[this.arr[15]]);
  if (this.arr[8] != -1)
  {
   this.arr[1] = 0;
   while ((long)this.arr[1] < 5L)
   {
    this.bitarr[2][this.arr[41]] = ((this.arr[8] & 1) != 0);
    this.arr[41]++;
    this.arr[8] = (int)((uint)this.arr[8] >> 1);
    this.arr[1]++;
   }
  }
  this.arr[15]++;
 }
 this.bitarr[1] = new BitArray(40);
 this.arr[61] = 0;
 this.arr[55] = 0;
 this.arr[24] = 0;
 while ((long)this.arr[24] < 40L)
 {
  this.arr[36] = (this.bitarr[0][this.arr[61]] ? 1 : 0);
  this.arr[61]++;
  this.arr[18] = 0;
  while ((long)this.arr[18] < 50L)
  {
   this.arr[19] = (this.bitarr[0][this.arr[61]] ? 1 : 0);
   if (this.arr[19] != 0)
   {
    this.arr[19] = (this.bitarr[2][this.arr[18]] ? 1 : 0);
    this.arr[36] += this.arr[19];
   }
   this.arr[61]++;
   this.arr[18]++;
  }
  this.arr[11] = 0;
  while ((long)this.arr[11] < 49L)
  {
   this.arr[47] = this.arr[11] + 1;
   while ((long)this.arr[47] < 50L)
   {
    this.arr[19] = (this.bitarr[0][this.arr[61]] ? 1 : 0);
    if (this.arr[19] != 0)
    {
     this.arr[19] = (this.bitarr[2][this.arr[11]] ? 1 : 0);
     this.arr[57] = (this.bitarr[2][this.arr[47]] ? 1 : 0);
     this.arr[57] *= this.arr[19];
     this.arr[36] += this.arr[57];
    }
    this.arr[61]++;
    this.arr[47]++;
   }
   this.arr[11]++;
  }
  this.bitarr[1][this.arr[55]] = ((this.arr[36] & 1) != 0);
  this.arr[55]++;
  this.arr[24]++;
 }
 this.bitarr[1].CopyTo(this.ans, 0);
}
[Full Code]
This can be further be hand optimized to convert all arrays to variables and while loops to for loop. The optimization will be done in a later step.

The key checking algorithm


As shown in Fig 7 the keygenme expects a username/password combination. It calculates a standard MD5 hash of the username, and compares some bytes of it to another hash computed from the password. The algorithm which implements the latter hash is the crux of this keygenme. For success, these comparisons must match.

Gimme the password!
Fig 7: Gimme the password!
The user supplied password is converted to a 50 size bit array using the following algorithm.
calc = new BitArray(50);

for (int i = 0, j = 0; i < password.Length; i++)
{
 int pos = "23456789ABCDEFGHJKLMNPQRSTUVWXYZ".IndexOf(password[i]);
 if (pos != -1)
 {
  for (int k = 0; k < 5; k++)
  {
   calc[j++] = (pos & 1) != 0;
   pos >>= 1;
  }
 }
}
Next, there is a huge hard coded byte array containing 6380 entries. This is also converted to a bit array. Since 8 bits make a byte, the size of the bit array is 6380 x 8 = 51,040.

Now, suppose the 50 bit password array is represented as p0, p1, p2, p3,......, p49. Using these two bit arrays, it calculates the value of 40 such following statements. The indices of the bits which are summed and multiplied are also fetched from the hard coded bit array. To understand how this is done refer to the decompiled code listing.
bit0 = (0 + p[1] + p[2] + p[9] + ... + p[49] + (p[0] * p[2]) + (p[0] * p[3]) + ... + (p[48] * p[49])) & 1;
bit1 = (1 + p[0] + p[2] + p[4] + ... + p[48] + (p[0] * p[2]) + (p[0] * p[3]) + ... + (p[48] * p[49])) & 1;
bit2 = (1 + p[0] + p[1] + p[2] + ... + p[49] + (p[0] * p[1]) + (p[0] * p[2]) + ... + (p[47] * p[49])) & 1;
...
37 more lines
...

The 40 calculated bits are then combined 8 at a time to form 5 bytes. For success, each byte thus obtained must match the corresponding byte obtained from the MD5 of the name as explained before.

Converting to a boolean system


The algorithm the keygenme implements is a sort of combination of a system of linear & bilinear equations having 50 unknowns (p0, ...p49). Note that in each of the equations only the last bit of the sum is retained, the remaining bits are discarded. Hence this can be converted to a boolean system, but before that we need to convert the arithmetic addition and multiplication operations to boolean logic. 

Converting arithmetic addition
In a boolean system, variables can have two possible values viz 0 or 1. Further, since we are only interested in the last bit, the result of addition operation will either be 0 or 1. We can either use a  Karnaugh map or a truth table. Here I used the latter.


Truth Table for Converting Bit Addition
A B F = A + B
0 0 0
0 1 1
1 0 1
1 1 0

A & B are two bits. Bit B is added to Bit A. The rightmost column denotes the sum. Using the above truth table to convert it to a canonical sum-of-products boolean expression we get the following which is already in its simplest form,


 Converting arithmetic product
Similar to addition, we can convert the product to an boolean expression,


Truth Table for converting Bit Product
A B C B.C F = A + B.C
0 0 0 0 0
0 0 1 0 0
0 1 0 0 0
0 1 1 1 1
1 0 0 0 1
1 0 1 0 1
1 1 0 0 1
1 1 1 1 0

Bit B & C are multiplied and added with Bit A. The rightmost column denotes the result. The canonical sum-of-products obtained is,


This can be further simplified to,


For simplification of boolean expressions,  there are online tools available such as http://www.32x8.com/ and http://tma.main.jp/logic/index_en.html.

An attempt at keygenning


The objective of the keygenme is thus to solve a system of equations having 50 unknowns. Now, as I said before that the de-virtualized code can further be hand optimized to get rid of the excess clutter. Here is it.
private void doIt()
{
 huge = new BitArray(hardcoded);
 calc = new BitArray(50);
 output = new BitArray(40);
 arr = new int[64];
 ans = new byte[5];

 for (int i = 0, j = 0; i < password.Length; i++)
 {
  int pos = "23456789ABCDEFGHJKLMNPQRSTUVWXYZ".IndexOf(password[i]);
  if (pos != -1)
  {
   for (int k = 0; k < 5; k++)
   {
    calc[j++] = (pos & 1) != 0;
    pos >>= 1;
   }
  }
 }

 for (int x = 0, y = 0; x < 40; x++)
 {
  bool bit = huge[y++];
  
  for (int a = 0; a < 50; a++)
   if (huge[y++])
    if (calc[a]) bit = !bit;

  for (int b = 0; b < 49; b++)
   for (int c = b + 1; c < 50; c++)
    if (huge[y++]) 
     if (calc[b] & calc[c]) bit = !bit;
  output[x] = bit;
 }
 output.CopyTo(ans, 0);
}
While loops have been converted to for loops. Arrays have been converted to variables. The last steps that remains is to develop a working keygen. For problems like this, I tend to prefer the Z3 SMT solver. Z3 has a nice python api to code against. Without further ado, here the is the code which tries to find a valid password for the name 0xec. It isn't a true keygen.
from z3 import *

from init_bits import initbits
from targ_bits import targbits
from sum_bits import sumbits
from prod_bits import prodbits

def main():
    bits = [Bool('b'+str(i)) for i in range(50)]
    s = SolverFor('sat') # Solver()
    keyspace = '23456789ABCDEFGHJKLMNPQRSTUVWXYZ'
    finalkey = ''
    tempkey = ''

    for i in range(len(initbits)):
        A = BoolVal(initbits[i])

        li = sumbits[i]
        for x in li:
            B = bits[x]
            A = Or(And(Not(A), B), And(A, Not(B)))

        li = prodbits[i]
        for x, y in li:
            B, C = bits[x], bits[y]
            A = Or(And(A, Not(B)), And(A, Not(C)), And(Not(A), B, C))

        s.add(A == targbits[i])
        print i


    if s.check() == sat:
        print 'Key Found!'
        m = s.model()
        for i in xrange(50):
            val = m[bits[i]]
            if val is not None:
                tempkey += '1'
            else:
                tempkey += '0'

        # Reverse tempkey
        tempkey = tempkey[::-1]
        for i in xrange(0, 50, 5):
            finalkey +=  keyspace[int(tempkey[i:i+5], 2)]

        finalkey = finalkey[::-1]
        print finalkey[0:5] + '-' + finalkey[5:]

    else:
        print 'Could not find a key:('

if __name__ == '__main__':
    main()
Congrats if you have read this far, however, I have disappointing news in store. The keygen developed does not generate a key within a realistic time. For a gold medal, we need to generate a key within one second. I have ran the keygen for more than an hour, and it still continued running. However, I know the code is correct since it can verify the sample username / password combinations (kao/QQRR9-DL6JF).

Further optimizations of the python code are possible. but that doesn't improve the situation. For example, if you closely look at the boolean expression for converting bit addition, you can deduce that it is the same as a 2 bit half adder where we are discarding the carry bit.


Similarly, the expression for converting bit product is a 3 bit full adder discarding the carry.

However, in spite of all of the above optimizations, it still remains unsolved.

Trying with an arithmetic system

As said before, the implemented algorithm is a combination of linear and bilinear system having 50 unknowns. In an arithmetic system, the problem looks like,


In simple maths, the above represents an equation similar to the following,


There are about 8 such equations. Each equation have a linear and a bilinear part. Without the bilinear part, we could have applied Gaussian Elimination for a solution, but that isn't the case to be. Further, my mathematical fu is not strong enough to devise an automated way to solve these type of equations. Hence, I will wait for others to solve this.
Posted by at
Labels: , , ,

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)