Reversing the petya ransomware with constraint solvers

With the advent of anonymous online money transactions (read Bitcoin) ransomware has become a profitable business in the cybercrime industry. This combined with the Tor network hides the attackers identity. Further, low infosec literacy makes social engineering really easy. All you need to do is send an email with an attached word file for a failed FedEx delivery etc. The victim would download the attachment, run the word file, enable macros, all without thinking a bit.

Minutes later he/she would be staring at a screen that may look like this

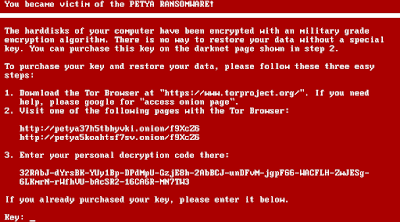Fig 1: The Petya lock screen

In panic, the hapless user may call his tech friend or google (seriously?) and be convinced that he/she has really lost all data. Now either he/she heed to the attacker's demands and pay the ransom or just forget it. Paying the ransom is however not too easy. There is no paypal, no credit card. The attackers accepts payments only in bitcoins and you also need to install the so called tor browser. This is the end of the road for many.

For us reversers, this is not the end. We try to find out if the user can have his/her data recovered WITHOUT paying the ransom. However this is not always possible particularly if the malware coders are experts. If not then we may have a way in just as was the case of the Petya ransomware which is the topic for today's blog post.

Preliminary Analysis

The sample on which the analysis has been done can be found here. 

The malware is different & unique from typical ransomware as it does not encrypts file. Instead it encrypts the MFT (Master File Table) on NTFS volumes. In short, on NTFS the MFT is a table which contains information about each and every file on the partition. For small files, the file content may be stored entirely within the MFT. For larger files, it contains a pointer to the actual data.

Encrypting the MFT is advantageous in the sense that the operation is very fast. You do not need to recursively traverse the entire drive to find the files. The files are there on the disk but the system does not know where to find them. This is as good as having the individual files encrypted.

The downside of having the MFT encrypted is the malware will need to be low level & sophisticated. Since the system cannot boot the OS a custom bootloader has to be developed. The code has to be 16-bit running in real mode. It has to use the BIOS interrupt services to communicate with the user. This is not an easy task considering we are used to develop in 32/64 bit with memory protection, segmentation and other niceties by the OS. In real mode we are responsible for everything.

Initial Triage

My favourite OS for reverse engineering tasks like this is old and trusty Windows XP. However for reasons unknown I could not get this sample running. Hence, I had to resort to a Windows 7 SP1 x86 VM. Running the sample leads to a BSOD after some seconds.

Fig 2: The BSOD

This BSOD is generated entirely from user mode by calling an undocumented API NtRaiseHardError. On the next boot a fake chkdsk scan starts to run.

Fig 3: The malware is hiding its action behind the fake scan.

In reality, the malware is doing its dirty work of encrypting the MFT. The chkdsk is just a decoy. When done we are presented with the redemption screen as in Fig 4 and then Fig 1. However it is not that scary as it looks :).

Fig 4: Danger Ahead!

Carving the mal-bootloader from disk

To perform static analysis we need the malicious bootloader. Since I have used vmware here, the easiest way would be to attach the vmware disk image (vmdk) to another virtual machine and use a tool like Active@ Disk Editor as in Fig 5. I have also developed a 010 editor template for parsing vmware disk images directly and can be used just in case.

Fig 5: Active Disk Editor in action

We need to the extract the sectors (first 10,000 sectors ~ 5 MiB should be more than enough) to a separate file.

IDA & Bochs

For static analysis we will be using IDA (no surprises). For dynamic analysis we will be using the Bochs debugger. Although vmware can debug bios code & bootloaders by its gdb stub but it is quite a pain to use efficiently. Hence we will stick with bochs. IDA provides first class support for bochs. Further running bochs is lot snappier than powering a full fledged vmware vm.

You can get the bxrc file (bochs config file) here. We can now load the bxrc file in IDA and it automatically do the rest.

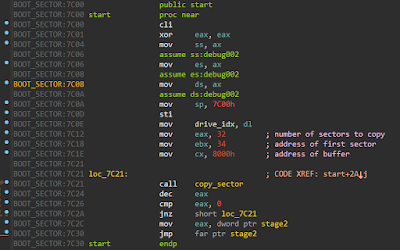Fig 6: The initial malware code

The malware copies 32 sectors starting from sector 34 to 0x8000 and jumps to it as in Fig 6.

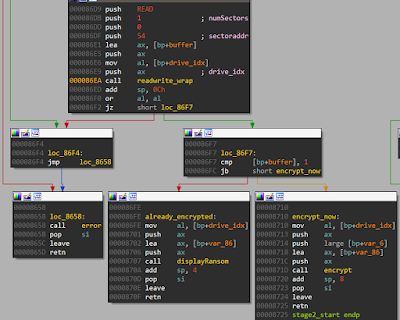Fig 7: To encrypt or not

Among other things, it reads sector 54 to a buffer. If the first byte contains 0 it proceeds to encrypt. If not it displays the ransom screen as shown in Fig 7. Hence the first byte of sector 54 is used mainly as a flag to decide its further course of action.

Analyzing the decryption code

We will be focussing primarily on the decryption algorithm. After all we are more interested in getting our data back than figuring out how it got lost. The process is simple, it reads a string, checks it and if it is valid decrypts our data.

Fig 8: Read & Check key

It accepts a key of maximum length 73 characters, but only the first 16 of them are used. The characters which are accepted consists of 1-9, a-z, A-X. After this the 16 byte key is expanded to a 32 byte key by adding 122 and doubling consecutive characters respectively. This is shown in Fig 9.

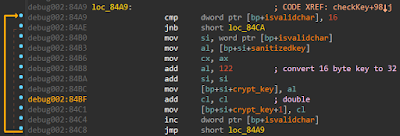Fig 9: Expanding the key

Next we reach the crux of the malware. It reads some data from sector 54 & 55 and passes them to the Crypt function. Using the 32 byte decryption key and an 8 byte Initialization Vector (nonce) from sector 54 it decrypts the 512 bytes of data in sector 55. If our key is correct, all byte in the decrypted data must equal all 0x37.

Fig 10: Calling Crypt

Finding the encryption algorithm

The encryption algorithm used is a variant of the Salsa stream cipher. I call this variant because properly implemented Salsa is quite secure. Well, how do we know this is Salsa? From magic constants, of course. See Fig 11.

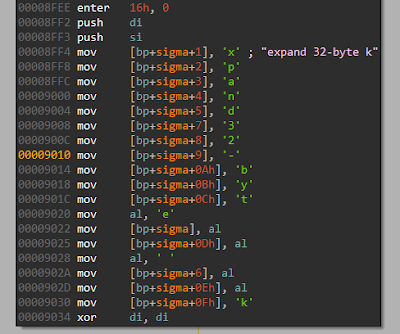Fig 11: expand 32-byte k

Searching for "expand 32-byte k" would directly lead you to Salsa. The exact code used in the malware can be found here. I am using the word exact in a broad sense. If it had been a ditto copy, we would have no chance of breaking it. The original Salsa implementation uses 32 bit (uint32_t) variables. This salsa implementation uses 16 bit variables for the same purpose borking it badly. Here is a snippet of the borked version. You can get the full version here. Compare this to the original version.

The primary reason for the mess up can be attributed to the fact that all of this is running in 16 bit real mode. So the authors decide to go easy and implement the exact same algorithm but with 16 bit variables.

Breaking the algorithm

We already have the entire algorithm in source code.  We need to fire up our tools to go & break it. These days, my defacto tool for such analysis has mostly been angr. However angr failed to work in this case. This is expected as the framework is in a continuous state of development. Not spending time on finding why it failed, I decided to look at other options. I used KLEE. It did not fail but took a long time and never finished. Next, some wild cropped up and I decided to use fuzzing based approach. For this I used the AFL framework. No luck here too.

Lastly I decided to use the tried and tested Z3 constraint solver and it did  not disappoint :). We already have the source, we just need to implement it in Z3. The code is as follows.

The program has  to be provided with the 8 byte nonce from sector 54. and 64 bytes from sector 55 after xoring with 0x37. The remainder of the program is a literal transcription of the c source and hence not explained. Running the program we get our decryption key in a few milliseconds. Apply the decryption key & hope for the best.

Fig 12: Mission accomplished!

Mission accomplished.

References

• http://blog.trendmicro.com/trendlabs-security-intelligence/petya-crypto-ransomware-overwrites-mbr-lock-users-computers/
• http://www.bleepingcomputer.com/news/security/petya-ransomware-skips-the-files-and-encrypts-your-hard-drive-instead/
• https://github.com/leo-stone/hack-petya
• http://pastebin.com/Zc16DfL1

Solving kao's toy project with symbolic execution and angr

Kao's toy project is a nifty and small crackme and quite ideal for demonstrating the power of symbolic execution. Running the crackme provides us with an installation id. We need to enter an unlock code which shows the goodboy message.

Fig 1: The main window

The installation id is calculated from the hard disk serial number. We will not focus on the algorithm that generates the installation id but rather on developing the keygen which calculates an unlock code when given an install id.

Before discussing about the function which checks the validity of the entered unlock code, it is important to mention that the installation id is 32 bytes (8 DWORDS) long and is displayed on the crackme screen in the form

D₁D₀-D₃D₂-D₅D₄-D₇D₆

i.e. within each QWORD the two DWORDS are stored in little endian order. We need to take this into account in our keygen program and convert the entered installation id to the proper form.

Previous Work

This crackme has previously been solved by Rolf Rolles who used a similar technique mentioned here in this blog post. While the method involving SMT solver is similar, Rolf used semi-automatic techniques, which translated the assembly code to IR and finally generated the constraints from the IR.

Before Rolf Rolles, this was solved by andrewl & Dcoder who used cryptanalysis techniques to reduce the keyspace. More recently, this was solved by Cr4sh who used the openreil framework.

The heart of the crackme

At the heart of the crackme lies this small function which checks whether a given unlock code is valid or not.

Fig 2: The checking function

The function takes two dwords (from the unlock code) as arguments which are then used to encode/encrypt the installation id (plaintext) to a given output buffer(ciphertext). For our entered unlock code to be valid, the encoded output must match the hardcoded string 0how4zdy81jpe5xfu92kar6cgiq3lst7.

Solving with Z3

At first we will try to model the system in Z3. Specifically, we will represent the encoding loop in Z3. Then we will use Z3 to solve the system and find the two dwords (unlock code) which encodes the installation id to the hardcoded string.

The script takes in the installation id as a command line argument. Lets' walk through the code step by step.

install_id = getInstallIdFromString(sys.argv[1])

Here we convert the install id into its proper form i.e the order of the two DWORDs within each QWORDs is reversed and returned as a list of integers.

target = map(ord, list('0how4zdy81jpe5xfu92kar6cgiq3lst7'))

After encoding the installation id it must match with the hardcoded string. Here we are converting the that string to a list of characters where each character is represented by its ASCII value.

part1 = edx = BitVec('part1', 32) 
part2 = ebx = BitVec('part2', 32)

We declare two bit-vectors of with a size of 32 bits each. These two bit vectors represents the two DWORDS of the unlock code.

for i in xrange(32):
    # text:00401105 lodsb
    byte = install_id[i]
        
    # text:00401106 sub al, bl
    byte -= Extract(7, 0, ebx)
    
    # text:00401108 xor al, dl
    byte ^= Extract(7, 0, edx)

    # text:0040110B rol edx, 1
    edx = RotateLeft(edx, 1)
        
    # text:0040110D rol ebx, 1
    ebx = RotateLeft(ebx, 1)
        
    # Add constraint
    s.add(byte == target[i])

The above loop describes the encoding process. Each character of the install_id is processed. This value must match the corresponding character in the target list. For this we use constraints.

# Solve the system
if s.check() == sat:
    m = s.model()
    print 'Unlock Code: ',
    print '%08X-%08X' %(m[part1].as_long(), m[part1].as_long () ^ m[part2].as_long())

Finally, we ask z3 to solve the system. and print the solutions.

Solving with angr

Okay we have already solved the crackme, so why another method? This is because I wanted to see if we can use angr for the same purpose, besides it would be a good learning experience.

Lets look at the cfg once again

Fig 3: We want to execute the green basic block and avoid the red one

At 40122A function check is called. If our entered unlock code is correct check would return 1 and we would go to the green color basic block at 401234 which displays the good boy message.

Now to the cfg of the check function.

Fig 4: Inserting hooks inside the check function

We are going to execute the above function symbolically. The unlock code which is comprised of two parts are passed as arguments to the function. Since we are executing this function in isolation we need provide the inputs ourselves, and this can be done by setting a hook at 4010FF (set_ebx_edx). Within the hook, we would store symbolic values representing the two parts of the unlock code into the ebx and edx registers.

Lastly, at 40111D there is a call to lstrcmpA. This function is imported from kernel32.dll.  Now, within our execution environment this dll is not loaded, we must emulate the behaviour of lstrcmpA and this can be done with SimProcedures.

Fig 5: lstrcmpA function

lstrcmpA is located at 40130E. We would set a hook at this location to call a SimProcedure which emulates the behaviour of lstrcmpA.

Now lets see the code which implements all of these.
Finally to wrap things up, here is an asciicast showing the solver in action.